|
Bank Angle and the Physics of Standard Rate Turns (continued)
VII - Standard Rate with TAS in Kilometers Per Hour (km/hr)
What about if TAS is in kilometers per hour (km/hr)? It is probably not necessary to go in detail over the whole process again, but here are the equations:
As before, we will keep acceleration of gravity (g) in m/s2 since it is the most common unit for g. For the remaining units the following table gives each unit and the number that it has to be multiplied by for it to be converted to SI units and used in equation 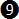 . .
Variables Used in Equation 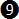 in Units in Units
Used in Aviation (Speed in km/hr) |
| |
| Name |
Symbol |
Aviation Unit |
Multiplier to
Convert to SI |
Exact Conversion |
| Bank Angle |
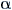 |
[o] |
(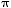 /180) /180) |
yes |
| Rate of Turn |
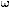 |
[o/s] |
(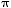 /180) /180) |
yes |
| Aircraft Speed |
v |
[km/hr] |
(5/18) |
yes |
 |
|
|
Table 7-1
Applying all the conversion multipliers in equation  we get: we get:
| |
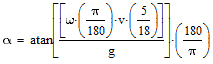 |
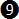 e e |
|
More user-friendly names for the symbols yields:
| |
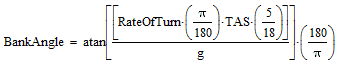 |
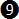 f f |
|
Reducing this equation to something more usable. Substituting: the Rate of Turn = 3o/s for standard rate; use the conventional standard for g, which is 9.80665 m/s2; and evaluating up to 5 significant digits we get:
Bank Angle = 57.296 · atan (0.0014831 · TAS) 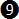 e e
Equation 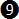 e gives the exact (with up to 5 significant digits of precision) bank angle in degrees for a standard rate turn. TAS is the true airspeed in km/h. e gives the exact (with up to 5 significant digits of precision) bank angle in degrees for a standard rate turn. TAS is the true airspeed in km/h.
Applying our simplification of arctangent, equation 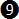 e becomes: e becomes:
Bank Angle  57.296 · 0.0014831 · TAS 57.296 · 0.0014831 · TAS
Now if we multiply the two numbers in our equation we will have:
Bank Angle  0.084976 · TAS 0.084976 · TAS 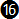
Equation 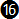 does not yield a nice rule of thumb formula with km/hr as it did with knots. Lets try some different formulas and try to figure out an easy way, if there is one, to calculate this estimate formula. does not yield a nice rule of thumb formula with km/hr as it did with knots. Lets try some different formulas and try to figure out an easy way, if there is one, to calculate this estimate formula.
We'll try the following equations that are easy to calculate and are somewhat close to equation 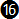 : :
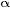 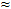 0.09 · TAS 0.09 · TAS 
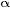  0.1 · TAS 0.1 · TAS 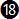
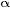  0.1 · TAS -2 0.1 · TAS -2 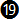
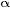 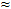 0.1 · TAS -10 0.1 · TAS -10 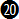
Comparing the Approximations for Standard Rate to the Exact Formula (in km/hr)
At Low Speeds:
| |
Standard Rate Turn Bank Angle (Low Speeds)
(TAS in km/hr)
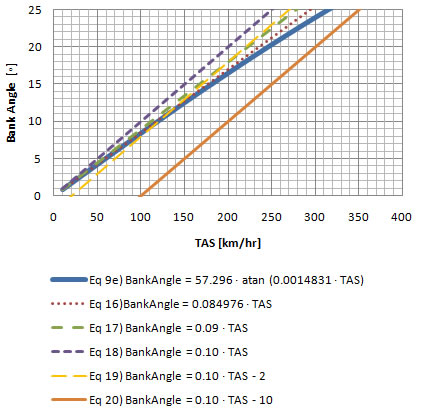 |
|
Chart 7-1
Chart 7-1 graphs each equation. The solid blue line is the exact equation  e. At a quick glance it seems that the only equations that are easy to calculate and remain close to the exact equation throughout this true airspeed (TAS) range are equations e. At a quick glance it seems that the only equations that are easy to calculate and remain close to the exact equation throughout this true airspeed (TAS) range are equations  and and  . .
| |
Standard Rate Turn Bank Angle Error (Low Speeds)
(TAS in km/hr)
 |
|
Chart 7-2
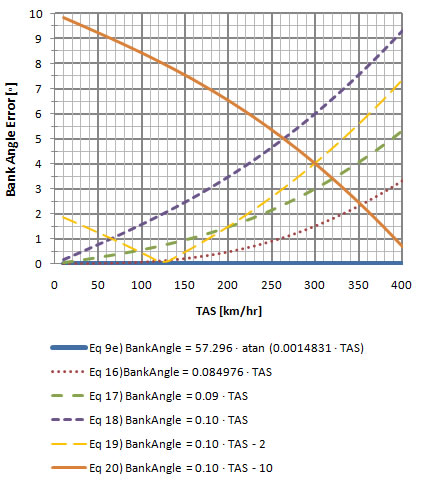
In chart 7-2 we can take a closer look at the deviations (errors) from the exact equation. Apart from the exact equation 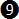 e, equation e, equation 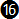 is the one with the least amount of error overall throughout the true airspeed range, but it is not easy to calculate mentally. Equation is the one with the least amount of error overall throughout the true airspeed range, but it is not easy to calculate mentally. Equation 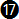 is more precise than equation is more precise than equation 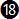 by almost two degrees. Ignoring equations by almost two degrees. Ignoring equations 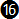 and and 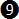 e, equation e, equation 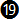 is more precise than the others throughout a range from about 100 to 200 km/hr; then equation is more precise than the others throughout a range from about 100 to 200 km/hr; then equation 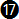 becomes more precise until about 320 km/hr; after that equation becomes more precise until about 320 km/hr; after that equation  is more precise but has an error of more than 5o after around 540 km/hr (see chart 7-4 below). is more precise but has an error of more than 5o after around 540 km/hr (see chart 7-4 below).
At High Speeds:
| |
Standard Rate Turn Bank Angle (High Speeds)
(TAS in km/hr)
 |
|
Chart 7-3
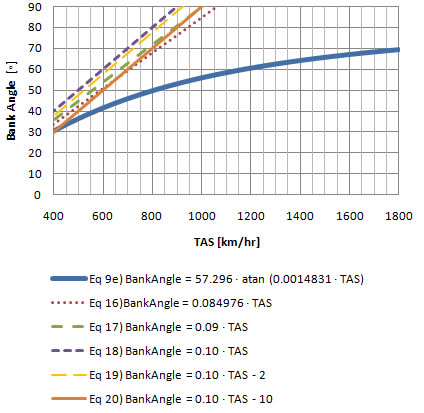
From chart 7-3 It looks like the bank angle passes 30o at around 400 km/hr. The chart below will give a better picture of the errors.
| |
Standard Rate Turn Bank Angle Error (High Speeds)
(TAS in km/hr)
 |
|
Chart 7-4
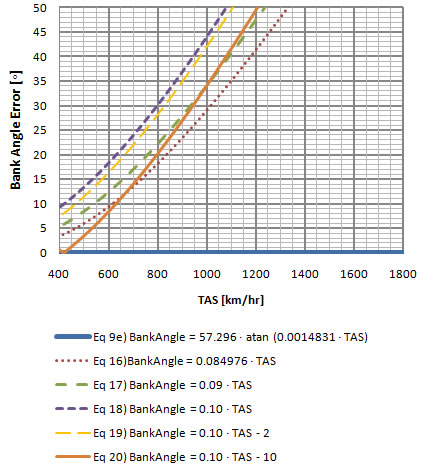
As mentioned previously, equation  is more precise from 320 km/hr but has an error of more than 5o after around 540 km/hr. is more precise from 320 km/hr but has an error of more than 5o after around 540 km/hr.
Conclusion:
The best equation will really depend on your speed range:
- From 10 - 100 km/hr equation
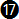 with a maximum error of 0.5o. with a maximum error of 0.5o.
- From 100 - 200 km/hr equation
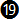 with a maximum error of 1.5o. with a maximum error of 1.5o.
- From 200 - 320 km/hr equation
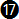 with a maximum error of 3.5o. with a maximum error of 3.5o.
- From 320 - 540 km/hr equation
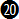 with a maximum error of 5o. with a maximum error of 5o.
To make things even simpler, if you don't mind a little more error from 100 - 200 knots, you can use:
- From 10 - 320 km/hr equation
 with a maximum error of 3.5o. with a maximum error of 3.5o.
- From 320 - 520 km/hr equation
 with a maximum error of 5o. with a maximum error of 5o.
|

