|
Bank Angle and the Physics of Standard Rate Turns
Table of Contents
I - Introduction
In this article we are going to look deep into standard rate turns and examine the math and some of physics behind them. We are also going to look at the "rule of thumb" (mental calculation) methods that pilots use to estimate the bank angle required to achieve a standard rate turn. We will verify how precise are they in comparison to an exact formula that we will construct. A basic knowledge of algebra and trigonometry is required to fully understand the rest of this article.
Defining Standard Rate Turn
Definition: A standard rate turn is maneuver in which an aircraft turns at a rate 3o per second (3o/s) .
If this turn is held for exactly two minutes (120 seconds) the aircraft will complete a 360o turn since:
3o/s · 120s = 360o
| Note: |
the middle dot (·) in the formula below means multiply. We will be using this notation throughout this text. |
The bank required to achieve standard rate changes with your true airspeed (TAS). The higher that speed, the greater the bank angle will need to be in order to achieve a standard rate turn.
| |
 |
 |
|
| |
(a) |
(b) |
|
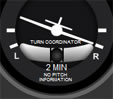
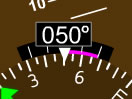
Fig 1-1 Instruments used to measure rate of turn in aircraft.
Figure 1-1 a shows an analog turn coordinator instrument that currently indicates a standard rate turn to the right (tip of the miniature aircraft wing on right marking). Figure 1-1 b shows the same situation on a digital display (magenta arc on second right marking). Note that these instruments are showing how fast the heading of the aircraft is changing (rate of turn). They do not show bank directly.
Estimating the Bank Angle to Achieve a Standard Rate Turn
| |
 |
 |
|
| |
(a) |
(b) |
|
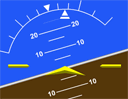
Fig 1-2 Attitude indicator instruments used to bank the aircraft.
When banking the aircraft to execute a standard rate turn, it is useful for pilots to have an approximate idea of how much that bank should be for standard rate. They will be using the attitude indicator (Figure 1-2 a & b) first to bank the aircraft and once they are at the approximate bank, they will then rely on the turn coordinator instrument (Figure 1-1 a & b) to adjust the initial bank so that a standard rate turn is established.
The following was taken directly from a paragraph in the FAA-H-8083-15A Instrument Flying Handbook, Page 5-19 and 5-20, 2008 Edition, published by United States Department of transportation, Federal Aviation Administration Air Men Testing Standards Branch:
"A rule of thumb to determine the approximate angle of bank required for a standard rate turn is to use 15 percent of the true airspeed. A simple way to determine this amount is to divide the airspeed by 10 and add one-half the result. For example, at 100 knots, approximately 15o of bank is required (100 ÷ 10 = 10 + 5 = 15); at 120 knots, approximately 18o of bank is needed for a standard rate turn."
in other words:
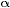 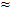 0.15 · TAS 0.15 · TAS
Where: 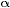 is the bank angle in degrees and TAS is the true airspeed in knots. This equation will later be referred to as equation is the bank angle in degrees and TAS is the true airspeed in knots. This equation will later be referred to as equation 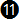 . .
| Note: |
the (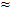 ) in the formula above means approximately. It will be used throughout this text to distinguish approximate formulas from the exact (=) formulas. ) in the formula above means approximately. It will be used throughout this text to distinguish approximate formulas from the exact (=) formulas. |
There are also some variations to this approximation method. One of them is:
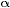 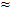 0.10 · TAS + 5 0.10 · TAS + 5
Basically meaning: take 10% of the true airspeed then add five to get the approximate bank angle in degrees for standard rate turn. This equation will later be referred to as equation 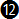 . .
|

