|
Bank Angle and the Physics of Standard Rate Turns (continued)
VI - Half Standard Rate Turns
Most pilots in heavier commercial aircraft normally don't exceed banks beyond 30o. However notice how in chart 5-3, in the previous section, that at slightly above 200 knots, the bank angle for standard rate will exceed 30o. To address this issue pilots will many times do a ½ standard rate turn. In other words instead of taking 2 minutes to complete a 360o turn, it will take 4 minutes.
For a ½ standard rate turn, since:
4 minutes = 4 · 60 seconds = 240 seconds
the aircraft will have to turn at a rate of:
360o / 240= 1.5o per second
Now we will go back to equation  b and plug-in 1.5o/s instead of 3o/s for the Rate of Turn: b and plug-in 1.5o/s instead of 3o/s for the Rate of Turn:
| |
 |
 b b |
|
Substituting: the Rate of Turn = 1.5o/s for standard rate; using the conventional standard value for g, which is 9.80665 m/s2; and evaluating up to 5 significant digits we get:
Bank Angle = 57.296 · atan (0.0013734 · TAS) 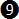 d (for ½ standard rate) d (for ½ standard rate)
which we will call equation 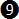 d. Applying our simplification of arctangent, equation d. Applying our simplification of arctangent, equation 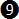 d becomes: d becomes:
Bank Angle  57.296 ·0.0013734· TAS (for ½ standard rate) 57.296 ·0.0013734· TAS (for ½ standard rate)
Now if we multiply the two numbers in our equation we will have:
Bank Angle  0.078685 · TAS 0.078685 · TAS 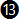 (for ½ standard rate) (for ½ standard rate)
The equation above is for a ½ standard rate turn. It is basically the same as taking the approximate equation  (below), from section IV, for the standard rate turn and dividing it by two (0.15737 / 2 = 0.078685). (below), from section IV, for the standard rate turn and dividing it by two (0.15737 / 2 = 0.078685).
Bank Angle  0.15737 · TAS 0.15737 · TAS  (for standard rate) (for standard rate)
Let's go ahead then and take the other equations that we used for standard rate turn ( 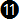 and and 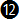 ) divide them by two and see how close we get to the bank bangle for ½ a standard rate turn given by the exact equation ) divide them by two and see how close we get to the bank bangle for ½ a standard rate turn given by the exact equation 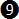 d. d.
| Bank Angle Equations for ½ Standard Rate Turn |
| |
| Equation Number |
Equation |
Exact |
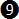 d d |
Bank Angle = 57.296 · atan (0.0013734 · TAS) |
yes* |
 |
Bank Angle  0.078685· TAS 0.078685· TAS |
no |
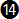 |
Bank Angle 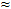 (0.15 · TAS) /2 (0.15 · TAS) /2 |
no |
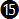 |
Bank Angle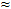 (0.10 · TAS + 5) /2 (0.10 · TAS + 5) /2 |
no |
| * Up to 5 significant digits |
 |
|
|
Table 6-1
The rule of thumb equations 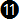 and and 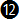 that we used for standard rate turn are now divided by two and called that we used for standard rate turn are now divided by two and called 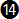 and and 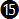 respectively. respectively.
Comparing the Approximations for ½ Standard Rate to the Exact Formula
At Low Speeds:
| |
½ Standard Rate Turn Bank Angle (Low Speeds)
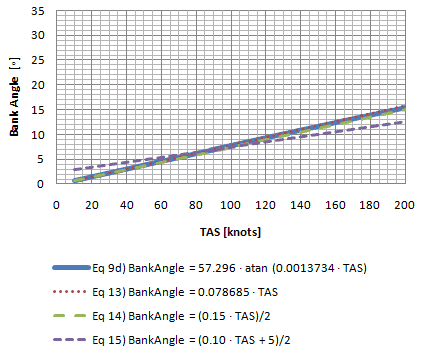 |
|
Chart 6-1
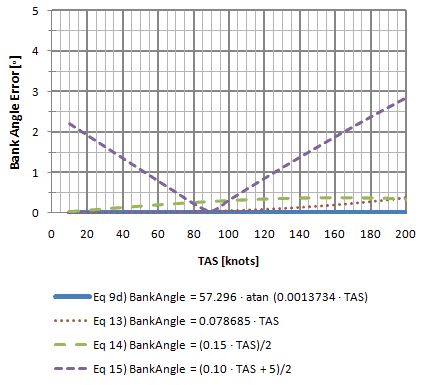
Chart 6-1 graphs each equation. The solid blue line is the exact equation 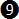 d. At a quick glance it seems that equation d. At a quick glance it seems that equation 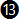 and and 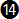 remain consistently close to the exact equation throughout the true airspeed (TAS) range. remain consistently close to the exact equation throughout the true airspeed (TAS) range.
| |
½ Standard Rate Turn Bank Angle Error (Low Speeds)
 |
|
Chart 6-2
In chart 6-2 we can take a closer look at the deviations from the exact equation (errors). Equation  is the one with the least amount of error overall throughout the true airspeed range but this equation is not easily used for mental calculation. Equation is the one with the least amount of error overall throughout the true airspeed range but this equation is not easily used for mental calculation. Equation  is more precise than equation is more precise than equation  but the difference is less than half a degree. Equation but the difference is less than half a degree. Equation 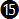 is only more precise than the others throughout a very narrow range from about 80 to 100 knots. is only more precise than the others throughout a very narrow range from about 80 to 100 knots.
At High Speeds:
| |
½ Standard Rate Turn Bank Angle (High Speeds)
 |
|
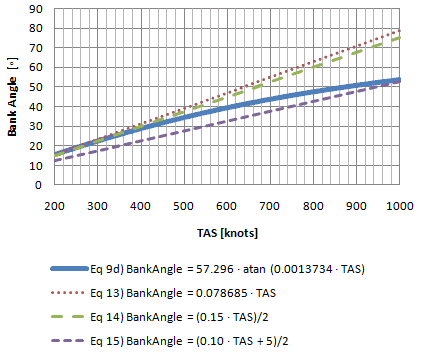
Chart 6-3
From chart 6-3 it looks like the bank angle passes 30o at around 420 knots. The chart below will give a better picture of the errors.
| |
½ Standard Rate Turn Bank Angle Error (High Speeds)
 |
|
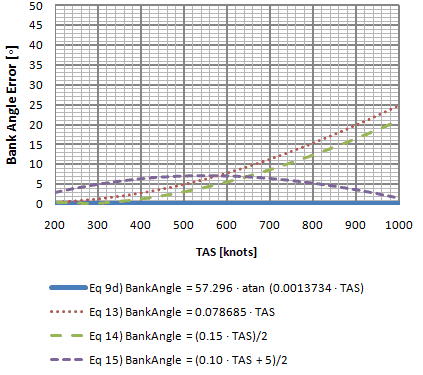
Chart 6-4
Chart 6-4 equation 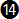 is better up to about 640 knots, however all equations are off by at least 7o at that point. Equation is better up to about 640 knots, however all equations are off by at least 7o at that point. Equation 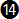 has an error of less than 5o up to about 580 knots and less than 2o at or below 400 knots. has an error of less than 5o up to about 580 knots and less than 2o at or below 400 knots.
Conclusion:
If you used equation 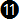 for estimating the bank angle for a regular standard rate turn, you can divide it by two (which yields equation for estimating the bank angle for a regular standard rate turn, you can divide it by two (which yields equation 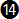 ) and get a pretty good estimate of the bank angle for ½ standard rate turn for speeds up to 400 knots (less than 2o error). ) and get a pretty good estimate of the bank angle for ½ standard rate turn for speeds up to 400 knots (less than 2o error).
|

