|
Calculating Sea-Level Barometric Correction
Most of the barometric pressure values that are listed on weather web sites are corrected to sea-level. This is done to standardize the values so that the altitude where the measurement was made does not significantly affect the result.
Barometric pressure that is not corrected to sea-level is usually referred to as absolute barometric pressure (the "absolute" term is what differentiates between the two) or absolute atmospheric pressure. The absolute atmospheric pressure is the actual pressure at the location where the measurement is taken from.
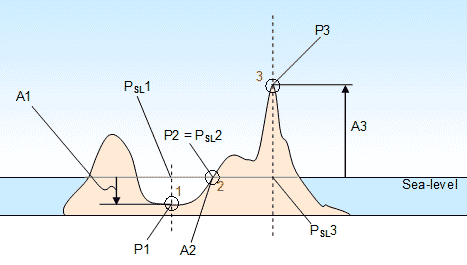
Suppose there are three locations on land that a pressure measurement is taken. Location 1 is below sea-level, location 2 is at sea-level and location 3 is above sea-level. If we know by looking at topographic maps, or other sources, what the absolute altitudes (A1, A2 and A3) of each location are and we measure the actual pressure (absolute atmospheric pressures P1, P2 and P3) at each location, we can calculate what would the pressures at sea-level (PSL1, PSL2 and PSL3) at each location. Below are the values we have:
| |
A1 = - 500 ft |
P1 = 31.20 inHg |
| |
A2 = 0 ft |
P2 = 30.65 inHg |
| |
A3 = 3000 ft |
P3 = 27.48 inHg |
Below are the values that we need to calculate. We can do each one individually because if we know A(absolute altitude) and P(absolute pressure) we can calculate PSL(pressure reduced to sea-level).
| |
PSL1 = ? |
|
| |
PSL2 = ? |
|
| |
PSL3 = ? |
|
Calculating PSL1:
Since we have the absolute atmospheric pressure, let us begin using the second calculator to get the pressure altitude based on the absolute atmospheric pressure.

Begin by highlighting the field that corresponds to the absolute atmospheric pressure in inHg.

Enter the 31.20 value and you get the pressure altitude of -1163 ft.

Moving back to the first calculator, highlight the field that corresponds to the pressure altitude.

Now enter the -1163 value that was just obtained.

Highlight the calibrated altitude* in ft.
| * |
Even though calibrated altitude and absolute altitude are not usually the same it is OK to assume they are in this case because we will be at the same altitude as the altimeter setting will be obtained. We will use the altimeter setting because it is equal to the barometric pressure reduced to sea-level when the location and altitude of measurement are the same. |

Enter -500 on the calibrated altitude in ft that is known for location 1.
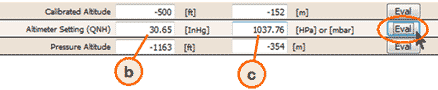
Press "Eval" on the remaining field which is Altimeter Setting (QNH) and read the answer 30.65 inHg on (b). You also get a result in HPa in (c). The barometric pressure (reduced to sea-level) is equivalent to the altimeter setting so PSL1 = 30.65 inHg.
Note that although the barometric pressure is equivalent to the altimeter setting, you should NEVER use the barometric pressure in place of the altimeter setting for flight. It may not be exactly the same because they are taken from different locations and the air pressure distribution may not be the same. Also, if they are taken from two different altitudes and atmospheric conditions are very different than standard atmosphere the correction to sea-level will be off because it is assuming standard atmosphere pressure distribution between where the measurement was taken and sea-level. Furthermore you can only obtain an altimeter setting from an official source approved for aviation use.
Calculating PSL2 and PSL3:
Calculating
PSL2 and PSL3 can be done in the same way as PSL1 so I leave it up to you to try. The answers are:
| |
PSL2 = 30.65 inHg |
|
| |
PSL3 = 30.65 inHg |
|
Notice that in this case PSL1 = PSL2 = PSL3 = 30.65 inHg. That is because the different locations are close enough so that the pressure and the air around them is evenly distributed. In practice the further the distance apart the more likely there are to be variations. That is OK, and you can still use this same method to calculate them and then compare each one to see where the high pressures and low pressure are in the region.
|

